看Prim算法之前要先知道什么是最小生成树。
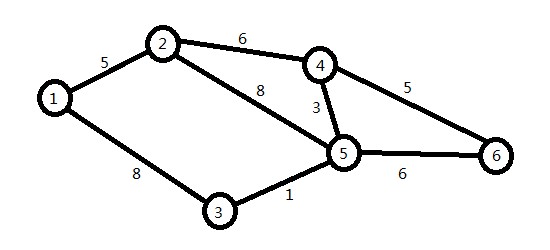
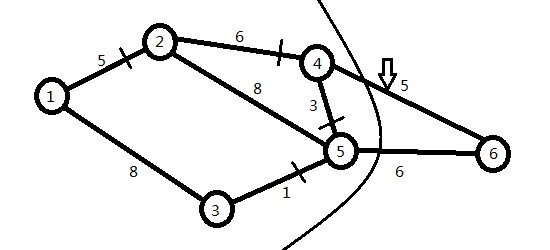
对于一个如下的图,求最小生成树的权值。
首先定义一个数组map[N][N](N根据题目决定大小)存放权值。对其进行初始化:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 0 | – | – | – | – | – | – | – |
| 1 | – | ∞ | 5 | 8 | ∞ | ∞ | ∞ |
| 2 | – | 5 | ∞ | ∞ | 6 | 8 | ∞ |
| 3 | – | 8 | ∞ | ∞ | ∞ | 1 | ∞ |
| 4 | – | ∞ | 6 | ∞ | ∞ | 3 | 5 |
| 5 | – | ∞ | 8 | 1 | 3 | ∞ | 6 |
| 6 | – | ∞ | ∞ | ∞ | 5 | 6 | ∞ |
接下来随便选一个点当起始点,程序中一般选择第一个点。这里我们选择点1作为起始点
然后定义两个数组,lowValue[N],mark[N]。mark是用来标记该点是否已走过,没走过标记为1,走过标记为0。
选择1作起点后应把1标记,此时mark为:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 1 | 1 | 1 | 1 |
而lowValue[i]表示已走过的点通往的点i的权值最小的路段权值。
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 5 | 8 | ∞ | ∞ | ∞ |
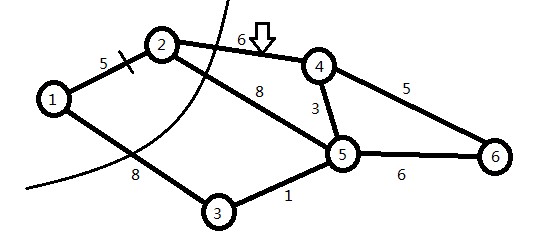
找出未走过的点即满足mark[i]==1时的最小值lowValue[i];此处i为2,lowValue[i]为5。
则标记2点为走过,更新mark:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 | 1 | 1 | 1 |
由于map[2][4]为6,map[2][5]为8,更新lowValue[4]=6;lowValue[5]为8
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 5 | 8 | 6 | 8 | ∞ |
得到下图
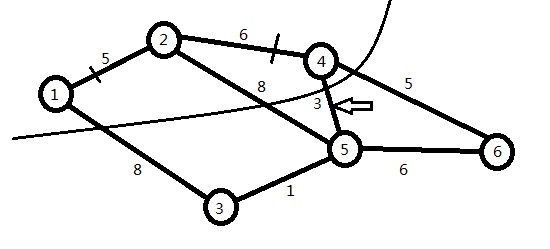
找出未走过的点即满足mark[i]==1时的最小值lowValue[i];此处i为4,lowValue[i]为6。
则标记4点为走过,更新mark:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 | 0 | 1 | 1 |
由于map[4][5]为3,map[4][6]为5,更新lowValue[5]=3;lowValue[6]为5
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 5 | 8 | 6 | 3 | 5 |
得到下图
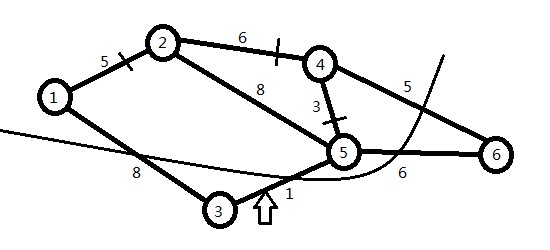
找出未走过的点即满足mark[i]==1时的最小值lowValue[i];此处i为5,lowValue[i]为3。
则标记5点为走过,更新mark:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 | 0 | 0 | 1 |
由于map[5][3]为1,map[5][6]为6,更新lowValue[3]=1。
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 5 | 1 | 6 | 3 | 5 |
得到下图
找出未走过的点即满足mark[i]==1时的最小值lowValue[i];此处i为3,lowValue[i]为1。
则标记3点为走过,更新mark:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 0 | 0 | 0 | 1 |
lowValue:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 5 | 1 | 6 | 3 | 5 |
得到下图
找出未走过的点即满足mark[i]==1时的最小值lowValue[i];此处i为6,lowValue[i]为5。
则标记6点为走过,更新mark:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 0 | 0 | 0 | 0 |
lowValue:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 5 | 1 | 6 | 3 | 5 |
得到下图
最后结果为lowValue中全部值的和20。
#include<stdio.h>
int main()
{
int map[111][111],lowValue[111],mark[111];
int i,j,n,m,x,y,z,min,s,t,ans,max=999999999;
while(scanf("%d%d",&n,&m),n){
for(i=1;i<=m;i++){
mark[i]=1;
lowValue[i]=max;
for(j=1;j<=m;j++){
map[i][j]=max;
}
}
while(n--){
scanf("%d%d%d",&x,&y,&z);
map[x][y]=map[y][x]=z;
}
ans=0;
for(s=i=1;i<m;i++){
mark[s]=0;
min=max;
for(j=1;j<=m;j++){
if(mark[j]&&map[s][j]<lowValue[j]){
lowValue[j]=map[s][j];
}
if(mark[j]&&min>=lowValue[j]){
min=lowValue[j];
t=j;
}
}
if(min==max){
break;
}
s=t;
ans+=min;
}
if(i==m){
printf("%d\n",ans);
}
else{
puts("?");
}
}
return 0;
}


0 条评论。